Some time ago I wrote an article on how to use a simple neural network in R with the neuralnet package to tackle a regression task. Since then, however, I turned my attention to other libraries such as MXNet, mainly because I wanted something more than what the neuralnet package provides (for starters, convolutional neural networks and, why not, recurrent neural networks).
A few weeks ago, however, I was asked how to use the neuralnet package for making a multilabel classifier. I wrote a quick script as an example and thought I could write a short article on it, furthermore I think a classification tutorial using the neuralnet package could be complementary to the one I did on regression.
The neuralnet package is perhaps not the best option in R for using neural networks. If you ask why, for starters it does not recognize the typical formula y~., it does not support factors, it does not provide a lot of models other than a standard MLP, and it has great competitors in the nnet package that seems to be better integrated in R and can be used with the caret package, and in the MXnet package that is a high level deep learning library which provides a wide variety of neural networks.
But still, I think there is some value in the ease of use of the neuralnet package, especially for a beginner, therefore I’ll be using it.
I’m going to be using both the neuralnet and, curiously enough, the nnet package. Let’s load them:
|
1 2 3 4 5 |
# load libs require(neuralnet) require(nnet) require(ggplot2) set.seed(10) |
The need for the nnet package will be more clear later on, I promise 😉
The dataset
I looked in the UCI Machine Learning Repository1 and found the wine dataset.
This dataset contains the results of a chemical analysis on 3 different kind of wines. The target variable is the label of the wine which is a factor with 3 (unordered) levels. The predictors are all continuous and represent 13 variables obtained as a result of chemical measurements.
This dataset seems not that hard to figure out, even the description says it is not quite challenging, but I think it is fine for practicing classification. Furthermore it is a little less boring than the iris dataset 😉
Loading the data
Simply download the dataset from the link above and save it as a .csv file in your working directory. Then you can load it in R as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Load data and set variables names wines <- read.csv("wines.csv") names(wines) <- c("label", "Alcohol", "Malic_acid", "Ash", "Alcalinity_of_ash", "Magnesium", "Total_phenols", "Flavanoids", "Nonflavanoid_phenols", "Proanthocyanins", "Color_intensity", "Hue", "OD280_OD315_of_diluted_wines", "Proline") head(wines) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
## label Alcohol Malic_acid Ash Alcalinity_of_ash Magnesium Total_phenols ## 1 1 13.20 1.78 2.14 11.2 100 2.65 ## 2 1 13.16 2.36 2.67 18.6 101 2.80 ## 3 1 14.37 1.95 2.50 16.8 113 3.85 ## 4 1 13.24 2.59 2.87 21.0 118 2.80 ## 5 1 14.20 1.76 2.45 15.2 112 3.27 ## 6 1 14.39 1.87 2.45 14.6 96 2.50 ## Flavanoids Nonflavanoid_phenols Proanthocyanins Color_intensity Hue ## 1 2.76 0.26 1.28 4.38 1.05 ## 2 3.24 0.30 2.81 5.68 1.03 ## 3 3.49 0.24 2.18 7.80 0.86 ## 4 2.69 0.39 1.82 4.32 1.04 ## 5 3.39 0.34 1.97 6.75 1.05 ## 6 2.52 0.30 1.98 5.25 1.02 ## OD280_OD315_of_diluted_wines Proline ## 1 3.40 1050 ## 2 3.17 1185 ## 3 3.45 1480 ## 4 2.93 735 ## 5 2.85 1450 ## 6 3.58 1290 |
Let’s have a look at a plot of some of the variables:
|
1 2 3 4 5 6 7 |
plt1 <- ggplot(wines, aes(x = Alcohol, y = Magnesium, colour = as.factor(label))) + geom_point(size=3) + ggtitle("Wines") plt2 <- ggplot(wines, aes(x = Alcohol, y = Proline, colour = as.factor(label))) + geom_point(size=3) + ggtitle("Wines") plt1 |
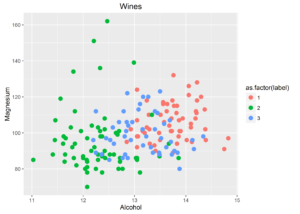
|
1 |
plt2 |
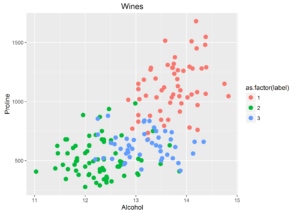
Out of the blue I decided to run PCA on the normalized dataset and found an interesting results worth displaying:
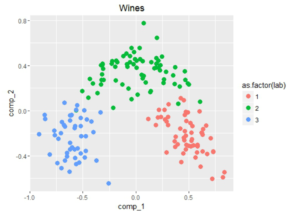
Although the first two components amount to about 50% of the total variance, it looks like it could be interesting to fit some classifier using only those two components. But let’s not get distracted by these beautiful plots, let’s go on to the next step.
Preprocessing
During the preprocessing phase, I have to do at least the following two things:
- Encode the categorical variables.
- Standardize the predictors.
First of all, let’s encode our target variable. The encoding of the categorical variables is needed when using neuralnet since it does not like factors at all. It will shout at you if you try to feed in a factor (I am told nnet likes factors though).
In the wine dataset the variable label contains three different labels: 1,2 and 3.
The usual practice, as far as I know, is to encode categorical variables as a “one hot” vector. For instance, if I had three classes, like in this case, I’d need to replace the label variable with three variables like these:
|
1 2 3 4 |
# l1,l2,l3 # 1,0,0 # 0,0,1 # ... |
In this case the first observation would be labelled as a 1, the second would be labelled as a 2, and so on. Ironically, the nnet package provides a function to perform this encoding in a painless way:
|
1 2 3 4 |
# Encode as a one hot vector multilabel data train <- cbind(wines[, 2:14], class.ind(as.factor(wines$label))) # Set labels name names(train) <- c(names(wines)[2:14],"l1","l2","l3") |
see? Very painless and fast! 😉
By the way, since the predictors are all continuous, you do not need to encode any of them, however, in case you needed to, you could apply the same strategy applied above to all the categorical predictors. Unless of course you’d like to try some other kind of custom encoding.
Now let’s standardize the predictors in the [0−1] interval by leveraging the lapply function:
|
1 2 3 4 |
# Scale data scl <- function(x){ (x - min(x))/(max(x) - min(x)) } train[, 1:13] <- data.frame(lapply(train[, 1:13], scl)) head(train) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
## Alcohol Malic_acid Ash Alcalinity_of_ash Magnesium Total_phenols ## 1 0.5710526 0.2055336 0.4171123 0.03092784 0.3260870 0.5758621 ## 2 0.5605263 0.3201581 0.7005348 0.41237113 0.3369565 0.6275862 ## 3 0.8789474 0.2391304 0.6096257 0.31958763 0.4673913 0.9896552 ## 4 0.5815789 0.3656126 0.8074866 0.53608247 0.5217391 0.6275862 ## 5 0.8342105 0.2015810 0.5828877 0.23711340 0.4565217 0.7896552 ## 6 0.8842105 0.2233202 0.5828877 0.20618557 0.2826087 0.5241379 ## Flavanoids Nonflavanoid_phenols Proanthocyanins Color_intensity ## 1 0.5105485 0.2452830 0.2744479 0.2645051 ## 2 0.6118143 0.3207547 0.7570978 0.3754266 ## 3 0.6645570 0.2075472 0.5583596 0.5563140 ## 4 0.4957806 0.4905660 0.4447950 0.2593857 ## 5 0.6434599 0.3962264 0.4921136 0.4667235 ## 6 0.4599156 0.3207547 0.4952681 0.3387372 ## Hue OD280_OD315_of_diluted_wines Proline l1 l2 l3 ## 1 0.4634146 0.7802198 0.5506419 1 0 0 ## 2 0.4471545 0.6959707 0.6469330 1 0 0 ## 3 0.3089431 0.7985348 0.8573466 1 0 0 ## 4 0.4552846 0.6080586 0.3259629 1 0 0 ## 5 0.4634146 0.5787546 0.8359486 1 0 0 ## 6 0.4390244 0.8461538 0.7218260 1 0 0 |
Fitting the model with neuralnet
Now it is finally time to fit the model.
As you might remember from the old post I wrote, neuralnet does not like the formula y~.. Fear not, you can build the formula to be used in a simple step:
|
1 2 3 4 |
# Set up formula n <- names(train) f <- as.formula(paste("l1 + l2 + l3 ~", paste(n[!n %in% c("l1","l2","l3")], collapse = " + "))) f |
|
1 2 3 4 |
## l1 + l2 + l3 ~ Alcohol + Malic_acid + Ash + Alcalinity_of_ash + ## Magnesium + Total_phenols + Flavanoids + Nonflavanoid_phenols + ## Proanthocyanins + Color_intensity + Hue + OD280_OD315_of_diluted_wines + ## Proline |
Note that the characters in the vector are not pasted to the right of the “~” symbol.
Just remember to check that the formula is indeed correct and then you are good to go.
Let’s train the neural network with the full dataset. It should take very little time to converge. If you did not standardize the predictors it could take a lot more though.
|
1 2 3 4 5 6 |
nn <- neuralnet(f, data = train, hidden = c(13, 10, 3), act.fct = "logistic", linear.output = FALSE, lifesign = "minimal") |
|
1 |
## hidden: 13, 10, 3 thresh: 0.01 rep: 1/1 steps: 88 error: 0.03039 time: 0.1 secs |
Note that I set the argument linear.output to FALSE in order to tell the model that I want to apply the activation function act.fct and that I am not doing a regression task. Then I set the activation function to logistic (which by the way is the default option) in order to apply the logistic function. The other available option is tanh but the model seems to perform a little worse with it so I opted for the default option. As far as I know these two are the only two available options, there is no “relu” function available although it seems to be a common activation function in other packages.
As far as the number of hidden neurons, I tried some combination and the one used seems to perform slightly better than the others (around 1% of accuracy difference in cross validation score).
By using the in-built plot method you can get a visual take on what is actually happening inside the model, however the plot is not that helpful I think
|
1 |
plot(nn) |
Let’s have a look at the accuracy on the training set:
|
1 2 3 4 5 6 |
# Compute predictions pr.nn <- compute(nn, train[, 1:13]) # Extract results pr.nn_ <- pr.nn$net.result head(pr.nn_) |
|
1 2 3 4 5 6 7 |
## [,1] [,2] [,3] ## [1,] 0.9897528761 0.003171322443 0.000006987838514 ## [2,] 0.9908394248 0.002331321781 0.000008693900073 ## [3,] 0.9914977585 0.002103254765 0.000008649814003 ## [4,] 0.9855622778 0.004418327885 0.000008738518880 ## [5,] 0.9916175055 0.002119520153 0.000008319926342 ## [6,] 0.9915542288 0.002144844815 0.000008337763696 |
|
1 2 3 4 |
# Accuracy (training set) original_values <- max.col(train[, 14:16]) pr.nn_2 <- max.col(pr.nn_) mean(pr.nn_2 == original_values) |
|
1 |
## [1] 1 |
100% not bad! But wait, this may be because our model over fitted the data, furthermore evaluating accuracy on the training set is kind of cheating since the model already “knows” (or should know) the answers. In order to assess the “true accuracy” of the model you need to perform some kind of cross validation.
Cross validating the classifier
Let’s crossvalidate the model using the evergreen 10 fold cross validation with the following train and test split: 95% of the dataset will be used as training set while the remaining 5% as test set.
Just out of curiosity I decided to run a LOOCV round too. In case you’d like to run this cross validation technique, just set the proportion variable to 0.995: this will select just one observation for as test set and leave all the other observations as training set. Running LOOCV you should get similar results to the 10 fold cross validation.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# Set seed for reproducibility purposes set.seed(500) # 10 fold cross validation k <- 10 # Results from cv outs <- NULL # Train test split proportions proportion <- 0.95 # Set to 0.995 for LOOCV # Crossvalidate, go! for(i in 1:k) { index <- sample(1:nrow(train), round(proportion*nrow(train))) train_cv <- train[index, ] test_cv <- train[-index, ] nn_cv <- neuralnet(f, data = train_cv, hidden = c(13, 10, 3), act.fct = "logistic", linear.output = FALSE) # Compute predictions pr.nn <- compute(nn_cv, test_cv[, 1:13]) # Extract results pr.nn_ <- pr.nn$net.result # Accuracy (test set) original_values <- max.col(test_cv[, 14:16]) pr.nn_2 <- max.col(pr.nn_) outs[i] <- mean(pr.nn_2 == original_values) } mean(outs) |
|
1 |
## [1] 0.9888888889 |
98.8%, awesome! Next time when you are invited to a relaxing evening that includes a wine tasting competition I think you should definitely bring your laptop as a contestant!
Aside from that poor taste joke, (I made it again!), indeed this dataset is not the most challenging, I think with some more tweaking a better cross validation score could be achieved. Nevertheless I hope you found this tutorial useful. A gist with the entire code for this tutorial can be found here.
Thank you for reading this article, please feel free to leave a comment if you have any questions or suggestions and share the post with others if you find it useful.
Notes:
1 Lichman, M. (2013). UCI Machine Learning Repository [http://archive.ics.uci.edu/ml]. Irvine, CA: University of California, School of Information and Computer Science.


Are you using the simple binary relevance method to perform the
multilabel classification? If yes, this is already available through
mlr, see the tutorial here:
http://mlr-org.github.io/mlr-tutorial/devel/html/multilabel/index.html
neuralnet is already implemented in mlr.
If it is more sophisticated, I maybe would be interested to implement it
in mlr as an “Algorithm adaptation method”.
In fact, I think this is a simple multiclass task in your example, isn’t it?
Hi Philipp, if by binary relevance method you mean training one classifier for each label, then no in this case I’m training a single classifier for all the labels, ie the output of the model is a vector of size 1xL real numbers in the 0-1 interval, where L is the number of labels (or Lx1 I cannot recall the if neuralnet uses column or row vectors, anyway I hope I got the point across). I did not know about mlr, thanks for pointing that out.
Yes, this is a simple multiclass task using a multi layer perceptron from the neuralnet package. The post was a reply to some questions I receveid on how to do a quick classification task with neuralnet (or with a MLP in R if you wish).